報 告 題 目：Liouville-type theorems and existence of solutions for quasilinear elliptic equations with nonlinear gradient terms

報 告 人：張正策 教授

報 告 時 間：2024年11月14日上午10:00

地點：太原理工大學明向校區伟德国际1916备用网址602

内容簡介：

In this talk, we consider two properties of positive weak solutions of quasilinear elliptic equation 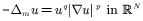, with nonlinear gradient terms. First, we show a Liouville-type theorem for positive weak solutions of the equation involving the m -Laplacian operator. The technique of Bernstein gradient estimates is ultilized to study the case p<m. Moreover, a Liouville-type theorem for supersolutions under subcritical range of exponents  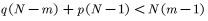is also established. Then, we use a degree argument to obtain the existence of positive weak solutions for a nonlinear Dirichlet problem of the type 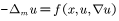, with f satisfying certain structure conditions. Our proof is based on a priori estimates, which will be accomplished by using a blow-up argument together with the Liouville-type theorem in the half-space. As another application, some new Harnack inequalities are proved. This is a joint work with Caihong Chang and Bei Hu.

報告人簡介：

張正策，2003年博士畢業于西安交通大學理學院，現任西安交通大學數學與統計學院教授，博士生導師，從事非線性偏微分方程理論及其應用研究。近年來, 主要對非線性抛物方程的梯度爆破和自由邊界問題開展定性研究，主持國家自然科學基金和省部級基金多項，在國際學術刊物CVPDE, JDE, DCDS, Siam J Numer Anal, NA等發表論文80餘篇。多次應邀參加CMSIC, AIMS和AMS Spring Section等國際學術會議并作報告，擔任美國數學會評論員。